[Python] 다이나믹 프로그래밍(9) - 1로 만들기

<문제> 1로 만들기: 문제 설명

• 정수 X가 주어질때 정수 X에 사용할 수 있는 연산은 다음과 같이 4가지입니다.

1) X가 5로 나누어떨어지면, 5로 나눕니다.

2) X가 3으로 나누어 떨어지면, 3으로 나눕니다.

3) X가 2로 나누어 떨어지면, 2로 나눕니다.

4) X에서 1을 뺀다.

• 정수 X가 주어졌을때, 연산 4개를 적절히 사용해서 1을 만들어야합니다. 이 연산을 사용하는 횟수의 최솟값을 출력하세요. 

X = 26일 경우
1. 26 - 1 = 25
2. 25 /5 = 5
3. 5 / 5 = 1

 

<문제> 1로 만들기: 문제조건

내코드

X = int(input())
count = 0

while X != 1:
    if X % 5 == 0:
        X /=5
        count +=1
    elif X % 5 <=1:
        X -=1
        count +=1
    elif X%3 == 0:
        X /=3
        count +=1
    elif X%3 <=1:
        X -=1
        count +=1
    elif X%2 == 0:
        X /=2
        count +=1
    elif X%2 <=1:
        X -=1
        count +=1

print(count)

<문제> 1로 만들기: 문제 해결 아이디어

• 피보나치 수열 문제를 도식화한 것처럼 함수가 호출되는 과정을 그림으로 그려보면 다음과 같습니다.

 

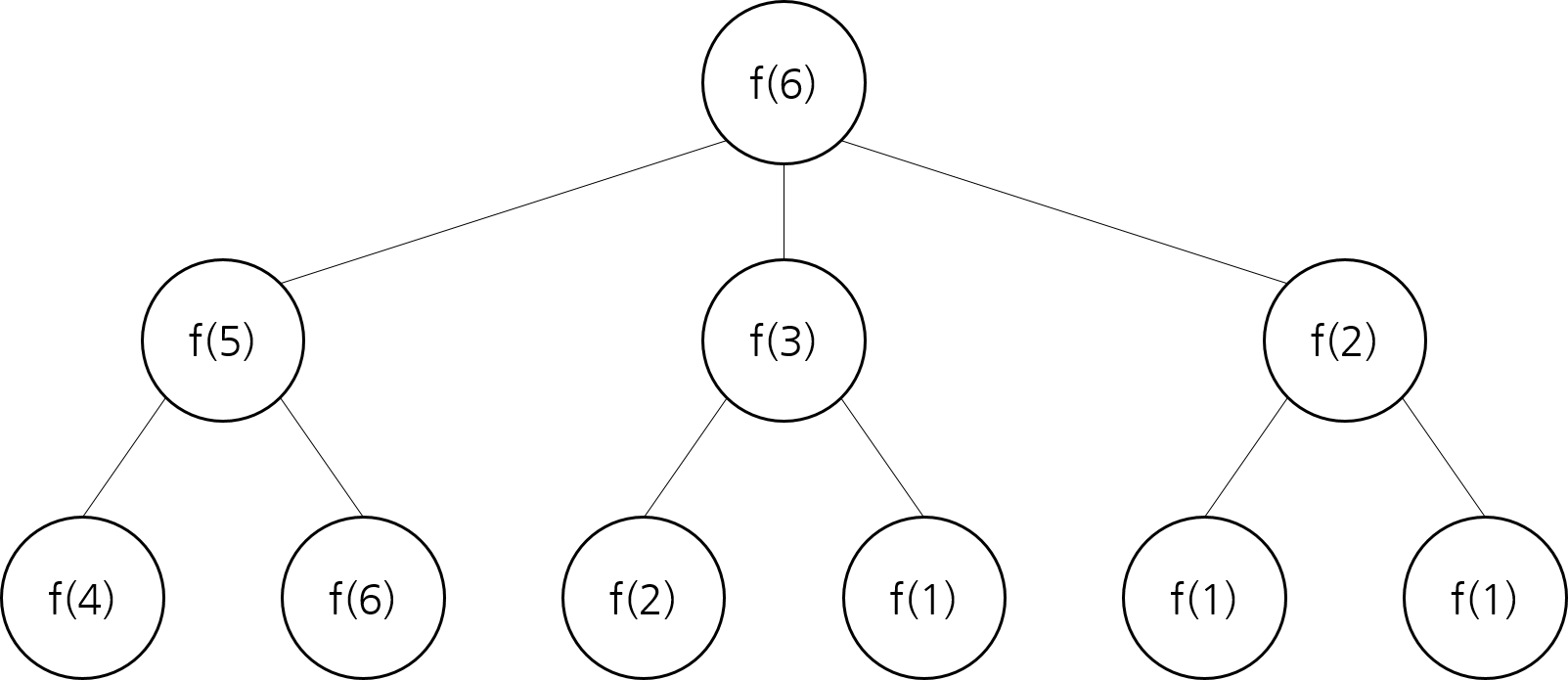
• 최적 부분 구조와 중복되는 부분 문제를 만족합니다.

• a_i = i를 1로 만들기 위한 최소 연산 횟수 점화식은 다음과 같다.

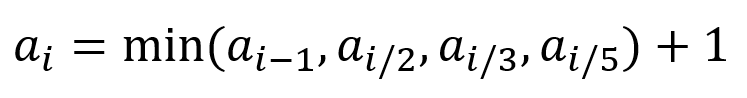
• 단, 1을 빼는 연산을 제외하고는 해당 수로 나누어떨어질 때에 한해 점화식을 적용할 수 있습니다.

x = int(input())

# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 30001

# 다이나믹 프로그래밍 진행 (보텀업)
for i in range(2, x+1):
    # 현재의 수에서 1을 빼는 경우
    # 1을 빼고 시작하는 이유 : 다음에 계산할 나누기에서 '1을 뺀 값'과 비교하여 횟수가 작은 것으로 교체될 것이기 때문에
    d[i] = d[i-1] + 1
    # 현재의 수가 2로 나누어 떨어지는 경우
    if i % 2 == 0:
        d[i] = min(d[i], d[i // 2] + 1) # 1을 더하는 이유 : d는 계산 횟수이기 때문, d[i]에 더하지 않는 이유는 위에서 1을 뺄 때 더해줬기 때문
    # 현재의 수가 3로 나누어 떨어지는 경우
    if i % 3 == 0:
        d[i] = min(d[i], d[i // 3] + 1)
    # 현재의 수가 5로 나누어 떨어지는 경우
    if i % 5 == 0:
        d[i] = min(d[i], d[i // 5] + 1)

print(d[x])